Python, Sean Clauson

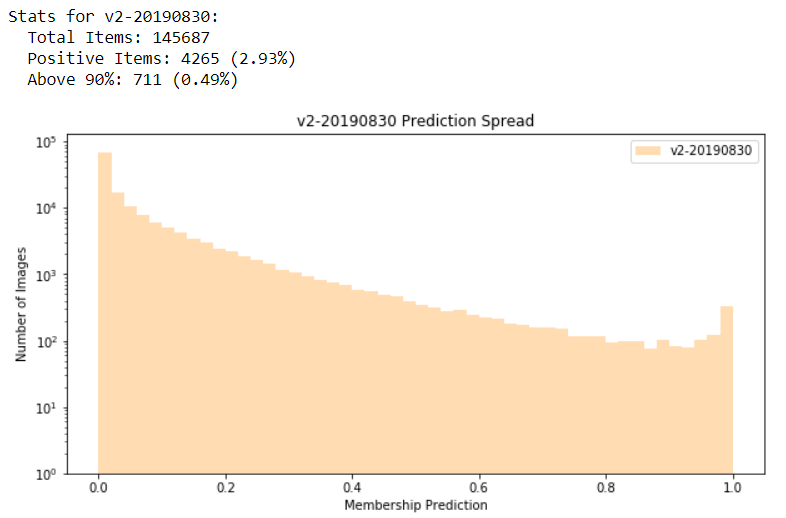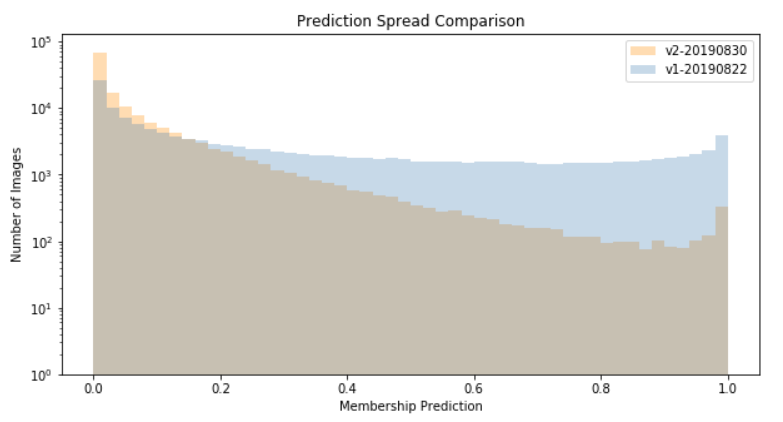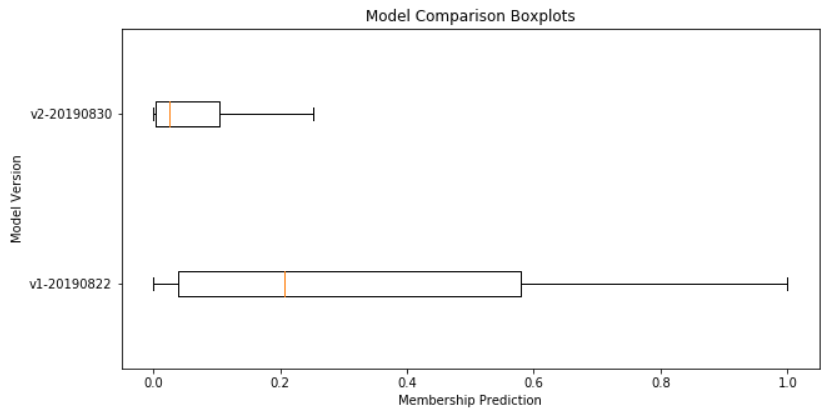
In support of some work related to color theory and linguistic relativity, I wrote some Python code to create visualizations of the RGB color space. A demo of some of the possible visualizations can be seen below (note, the animated GIF was created using GIMP):

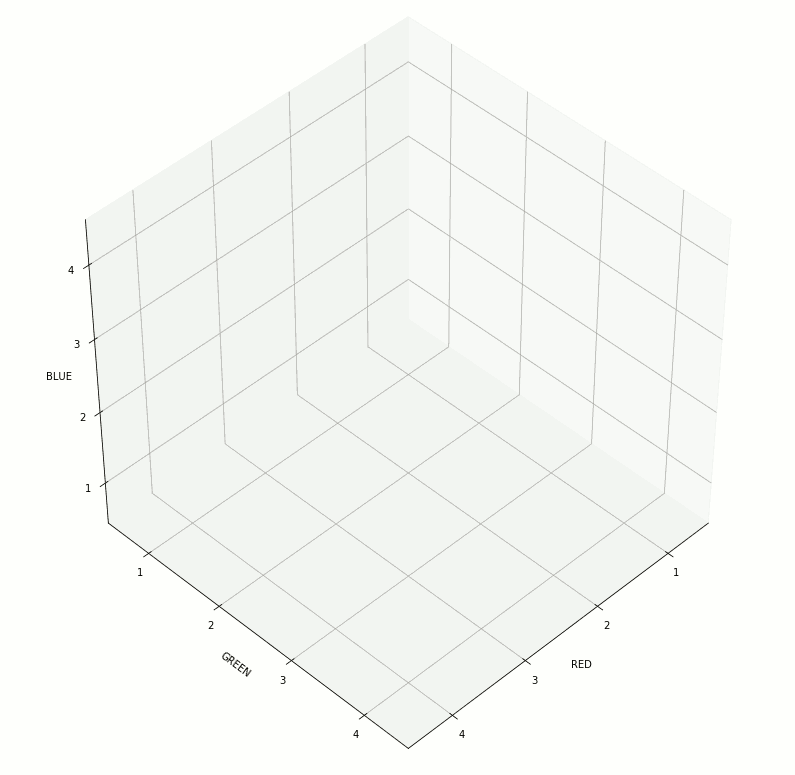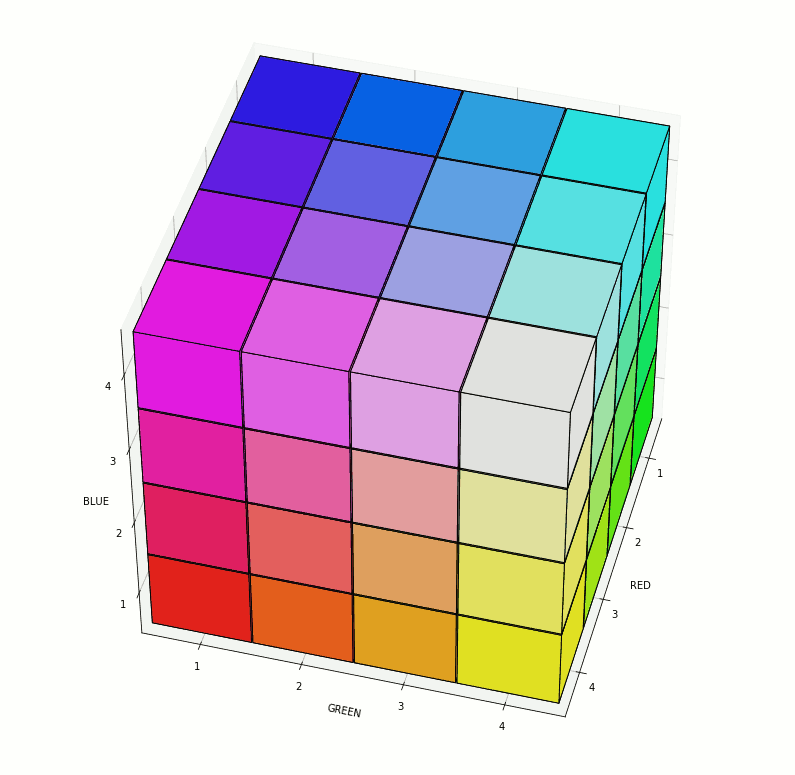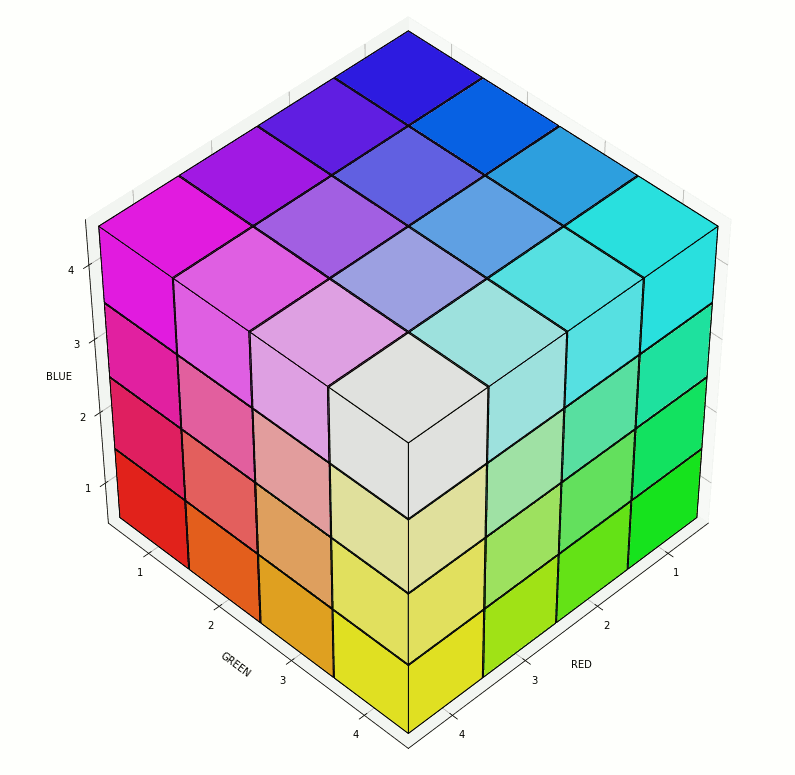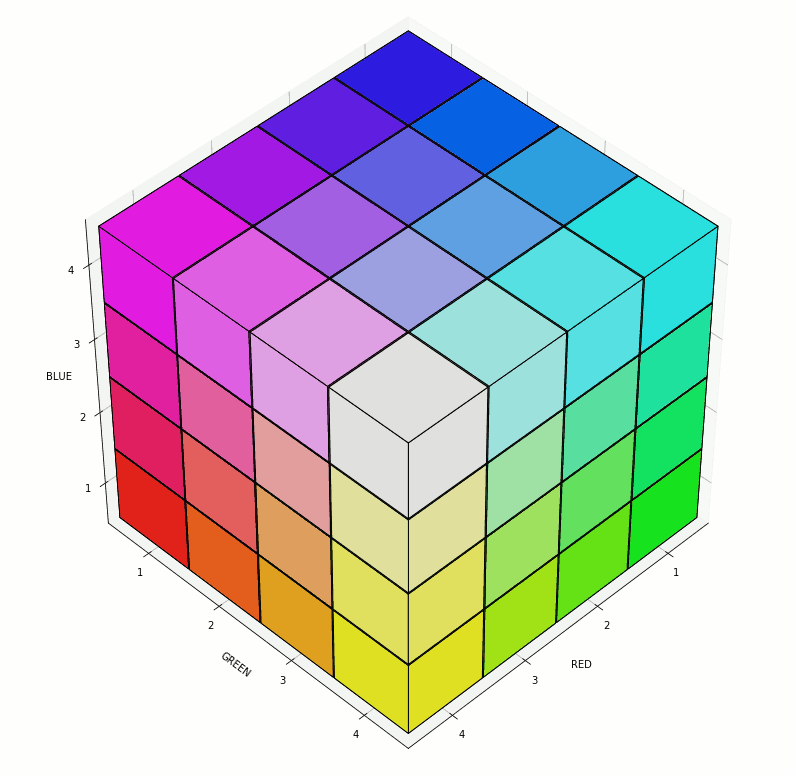
The relevant code follows (Python 3.7):

%matplotlib inline

import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from mpl_toolkits.mplot3d.art3d import Poly3DCollection
import random
import copy

def get_color_verts(r_rng, g_rng, b_rng):
    """
    Given a range in the RGB space, compiles list of vertices to be drawn.
    Used to draw the cubes representing each of the 64 defined colors.
    """
    r_min, r_max = r_rng
    g_min, g_max = g_rng
    b_min, b_max = b_rng
    # In order: r+g wrt-b, r+b wrt-g, g+b wrt-r 
    verts = [[(r_max,g_min,b_min),(r_max,g_max,b_min),(r_min,g_max,b_min),(r_min,g_min,b_min)],
             [(r_max,g_min,b_max),(r_max,g_max,b_max),(r_min,g_max,b_max),(r_min,g_min,b_max)],
             [(r_max,g_min,b_min),(r_max,g_min,b_max),(r_min,g_min,b_max),(r_min,g_min,b_min)],
             [(r_max,g_max,b_min),(r_max,g_max,b_max),(r_min,g_max,b_max),(r_min,g_max,b_min)],
             [(r_min,g_min,b_max),(r_min,g_max,b_max),(r_min,g_max,b_min),(r_min,g_min,b_min)],
             [(r_max,g_min,b_max),(r_max,g_max,b_max),(r_max,g_max,b_min),(r_max,g_min,b_min)]
            ]
    return verts

def get_color_middle(r_rng, g_rng, b_rng):
    """
    Given a range in the RGB space, returns the color represented by the center point of the cube.
    Used to draw the color of a given cube.
    """
    r_min, r_max = r_rng
    g_min, g_max = g_rng
    b_min, b_max = b_rng
    return (((r_min+r_max)/2)/255.0, ((g_min+g_max)/2)/255.0, ((b_min+b_max)/2)/255.0)

def get_random(min_val, max_val):
    return random.randint(min_val, max_val)

def get_random_color(r_rng, g_rng, b_rng):
    """
    Given a range in the RGB space, selects a random point within the cube and returns the associated color.
    Used to draw random points within each shown cube.
    """
    val = [get_random(r_rng[0], r_rng[1]),
           get_random(g_rng[0], g_rng[1]),
           get_random(b_rng[0], b_rng[1])]
    return val

def adjust_points_per_cube(orig, color_list):
    """
    Depending on the number of colors which will be drawn, adjust the number of points shown in each.
    Used to balance performance.
    """
    ret = orig
    if orig == 0:
        if not color_list or len(color_list) > 8:
            ret = 50
        elif len(color_list) == 1:
            ret = 1000
        elif len(color_list) <= 3:
            ret = 500
        elif len(color_list) <= 8:
            ret = 300    
    return ret

def get_filtered_color_list(all_colors, inc_colors):
    ret = []
    if not inc_colors:
        ret = copy.deepcopy(all_colors)
    else:
        for c in all_colors:
            if c["key"] in inc_colors:
                ret.append(c)
    return ret  
       
def set_axis_limits(ax, show_full_grid, color_list):
    """
    Calculates the limits of each axis, depending on which subset of the RGB space is being shown.
    """
    if show_full_grid:
        ax.set(xlim3d = (0, 255), ylim3d = (0, 255), zlim3d = (0, 255))
    else:
        # Get min/max for chart limits (start w/inverse)
        r_min, r_max, g_min, g_max, b_min, b_max = [255, 0, 255, 0, 255, 0]
        for c in color_list:
            r_min = min(r_min, c["r"][0])
            g_min = min(g_min, c["g"][0])
            b_min = min(b_min, c["b"][0])
            r_max = max(r_max, c["r"][1])
            g_max = max(g_max, c["g"][1])
            b_max = max(b_max, c["b"][1])
            # ax.set(xlim3d = (r_min, r_max), ylim3d = (g_min, g_max), zlim3d = (b_min, b_max))
            ax.set(xlim3d = (r_min-5, r_max+5), ylim3d = (g_min-5, g_max+5), zlim3d = (b_min-5, b_max+5))    

def draw_random_points(points_per_cube, color_list):
    for col in color_list:
        for i in range(points_per_cube):
            ci = get_random_color(col["r"], col["g"], col["b"])
            area = (15)**2
            ax.scatter(ci[0], ci[1], ci[2], 
                       color = [ci[0]/255.0, ci[1]/255.0, ci[2]/255.0], 
                       s = area)

def draw_cubes(ax, color_list, hilite_list, cube_alpha, hilite_alpha, edge_color):
    for c in color_list:
        p = Poly3DCollection(get_color_verts(c["r"], c["g"], c["b"]), alpha = cube_alpha)
        p.set_color(get_color_middle(c["r"], c["g"], c["b"]))
        if c["key"] in hilite_list:
            p.set_alpha(hilite_alpha)
        if edge_color:
            p.set_edgecolor(edge_color)
        ax.add_collection3d(p)            
            
def set_axis_tickmarks(ax, x, y, z):
    ax.set_xticks(x)
    ax.set_yticks(y)
    ax.set_zticks(z)
    
def set_axis_ticklabels(ax, x, y, z):
    ax.set_xticklabels(x)
    ax.set_yticklabels(y)
    ax.set_zticklabels(z)    

def create_color_list():
    """
    Creates a list of 64 "colors", by evenly dividing RGB space into 64 equal-sized cubes.
    This is accomplished by dividing each axis (R, G, B) into quarters.
    """
    # NOTE: A 3-character "key" is used to identify each of the 64 cubes. Used in filtering the display.
    keys_ = [["B", "G", "L", "M"],["A", "E", "I", "O"],["R", "S", "T", "V"]]
    rng_ = [[0, 63], [64, 127], [128, 191], [192, 255]]

    colors = []
    for idx_r, rng_r in enumerate(rng_):
        for idx_g, rng_g in enumerate(rng_):
            for idx_b, rng_b in enumerate(rng_):
                color = {}
                color["key"] = "{}{}{}".format(keys_[0][idx_r], keys_[1][idx_g], keys_[2][idx_b])
                color["r"] = rng_r
                color["g"] = rng_g
                color["b"] = rng_b
                colors.append(color)
    
    return colors    
 
colors = create_color_list()

show_boxes = True       # Determines whether surfaces of each defined color cube is drawn.
show_points = True     # Set to True to draw random points of example shades in each selected cube.
points_per_cube = 0     # Number of random shades to draw. Set to 0 to use defaults, which balances for performance.
box_alpha = .1         # Alpha value for all shown colors.
hilite_alpha = 1.0      # Alpha value used for colors found in hilite_cubes list.
edge_color = [0, 0, 0]  # Color used to draw the edges of vertices.
show_full_grid = False   # Setting to False will focus space on just the shown cubes.
color_filter = []       # Keys of colors to be included. Set to empty [] to include all colors.
hilite_cubes = []       # Keys of colors to hilight (will use hilite_alpha value). Ignored if empty [].

points_per_cube = adjust_points_per_cube(points_per_cube, color_filter)

x_colors = []
x_colors = get_filtered_color_list(colors, color_filter)        
            
fig = plt.figure(figsize = [14, 14])
ax = fig.gca(projection = '3d')

set_axis_limits(ax, show_full_grid, x_colors)
ax.set(xlabel = "RED", ylabel = "GREEN", zlabel = "BLUE")

ticks_ = [32, 96, 160, 223]
set_axis_tickmarks(ax, x=ticks_, y=ticks_, z=ticks_)

ticklbl_ = ["1", "2", "3", "4"]
set_axis_ticklabels(ax, x=ticklbl_, y=ticklbl_, z=ticklbl_)
         
if show_points:
    draw_random_points(points_per_cube, x_colors)
    
if show_boxes:
    draw_cubes(ax, x_colors, hilite_cubes, box_alpha, hilite_alpha, edge_color)
    
ax.view_init(45, 45)  

# fig.savefig("demo-1.png", bbox_inches = "tight")

Lorem ipsum

This post documents the code used to compare model iterations, as described in the post “Bootstrapping Model Data“. The code is written in Python 3.7.

Input

This code is currently comparing the results of 2 models. The results for each model are stored in a JSON file, which contains the model’s prediction for each image in my full image set.

An example of this JSON file follows:

[
    {
        'path': 'D:\\Roots\\oai-images\\00000000-0000-0000-0000-000000000000-roots-1.jpeg',
        'value': 'negative',
        'conf': 0.72014
    },
    ....
]

This snippet shows the stored prediction for one image. Each saved prediction includes:

The path of the image used to make this prediction.
The value of the prediction made by the model. In this example, value will either be “positive” or “negative” depending on whether the image contains a picture of a bridge or not (respectively).
The confidence of the model’s prediction (conf).

Output

For each model, I’m outputting some very basic stats of the predictions (output_stats) and a histogram which shows the spread of the predictions (plot_histogram):

Next, I’m outputting a combined histogram of all models (plot_histogram):

Finally, I’m also plotting the results of all models as a box plot (plot_boxplot):

Code

Here is the code used to generate these visualizations, in Python 3.7. Note that this is prototype, and not production-ready…

import matplotlib.pyplot as plt
import json

def get_json_from_path(file_path):
    json_data = json.loads(open(file_path).read())
    return json_data


def get_membership_value(item):
    if item["value"] == "negative":
        return 1 - item["conf"]
    else:
        return item["conf"]


def plot_histogram(data, title, xlabel, ylabel, label, color, log = False):
    plt.figure(figsize = (10, 5))
    _ = plt.hist(data, bins = 50, log = log, histtype = "stepfilled", alpha = 0.3, label = label, color = color)

    plt.legend(prop={'size': 10})
    plt.ylim(bottom=1)
    plt.title(title)
    plt.xlabel(xlabel)
    plt.ylabel(ylabel)
    plt.show()   

    
def plot_boxplot(data, title, xlabel, ylabel, label):
    plt.figure(figsize = (10, 5))
    _ = plt.boxplot(data, labels = label, vert = False, showfliers = False)
    plt.title(title)
    plt.xlabel(xlabel)
    plt.ylabel(ylabel)
    plt.show()


def output_stats(data, name):    
    total_count = len(data)
    pos_count = 0
    pos_gt90_count = 0
    for item in data:
        if item > 0.5:
            pos_count += 1
            if item >= 0.9:
                pos_gt90_count += 1
    
    print("Stats for {}:".format(name))
    print("  Total Items: {}".format(total_count))
    print("  Positive Items: {0} ({1:.2f}%)".format(pos_count, pos_count / total_count * 100))
    print("  Above 90%: {0} ({1:.2f}%)".format(pos_gt90_count, pos_gt90_count / total_count * 100))

 
v1res_path = r"D:\Roots\model-predictions\roots-Contains-Structure-Bridge-20190822-vl0p23661.json"
v2res_path = r"D:\Roots\model-predictions\roots-Contains-Structure-Bridge-20190830-vl0p29003.json"

v1_results = list(map(get_membership_value, get_json_from_path(v1res_path)))
v2_results = list(map(get_membership_value, get_json_from_path(v2res_path)))

data = (v1_results, v2_results)
names = ("v1-20190822", "v2-20190830")
colors = ("steelblue", "darkorange")

for i in range(0, len(names)):
    output_stats(data[i], names[i])
    plot_histogram(data[i], "{} Prediction Spread".format(names[i]), "Membership Prediction", "Number of Images", label = names[i], log = True, color = colors[i])

plot_histogram(data, "Prediction Spread Comparison", "Membership Prediction", "Number of Images", label = names, log = True, color = colors)

plot_boxplot(data, "Model Comparison Boxplots", "Membership Prediction", "Model Version", label = names)

Full-Stack Engineer and Technology Leadership

Color Space – Visualizations

Bootstrapping Model Data – Visualization

Input

Output

Code